Différences entre les versions de « Numération »
(Comment les ordinateurs gèrent les nombres) |
|||
| (3 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
Les système de numération | |||
== Le binaire == | |||
Le processeur en lui-même ne gère que des bits. On dit qu'il utilise le système binaire. | Le processeur en lui-même ne gère que des bits. On dit qu'il utilise le système binaire. | ||
On résume souvent au zéro (0) et au un (1) pour distinguer les deux états. Ceci est bien pratique pour réaliser des calculs. | On résume souvent au zéro (0) et au un (1) pour distinguer les deux états. Ceci est bien pratique pour réaliser des calculs. | ||
| Ligne 17 : | Ligne 17 : | ||
D'autres opérateurs existent mais en réalité ils peuvent être construit à partir des 3 précédents: XOU ou OU exclusif, NAND ou NOT AND, IMP ou implication. | D'autres opérateurs existent mais en réalité ils peuvent être construit à partir des 3 précédents: XOU ou OU exclusif, NAND ou NOT AND, IMP ou implication. | ||
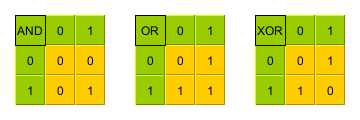
[[Fichier:Portes logiques.png|cadre|Principales portes logiques]] | |||
=== Le ET logique === | |||
La sortie du ET est vraie si et seulement si les 2 entrées sont vraies. | La sortie du ET est vraie si et seulement si les 2 entrées sont vraies. | ||
Il est souvent noté par le point. | Il est souvent noté par le point. | ||
=== Le OU logique === | |||
La sortie du OU est vraie si et seulement si l'une des 2 entrées au moins est vraie. | La sortie du OU est vraie si et seulement si l'une des 2 entrées au moins est vraie. | ||
Il est souvent noté par le signe plus (+). | Il est souvent noté par le signe plus (+). | ||
=== Le NON logique === | |||
La sortie du NON est toujours l'opposé de l'entrée. | La sortie du NON est toujours l'opposé de l'entrée. | ||
Il est représenté par une barre horizontale au-dessus de l'expression. | Il est représenté par une barre horizontale au-dessus de l'expression. | ||
== Les entiers == | |||
Une succession de 0 et de 1 c'est bien joli, mais ce n'est pas trop parlant pour un humain qui à l'habitude de manipuler les nombres en base décimale. | Une succession de 0 et de 1 c'est bien joli, mais ce n'est pas trop parlant pour un humain qui à l'habitude de manipuler les nombres en base décimale. | ||
Pour stocker des nombre entiers nous utilisons des regroupements de bits: | Pour stocker des nombre entiers nous utilisons des regroupements de bits: | ||
* le tercet: permet de représenter des chiffres de 0 à 7 en base octale (base 8). | |||
* le quartet: permet de représenté un chiffre hexadécimal de 0 à F (0 à 15 en décimal). | |||
* le septet: représente des nombres de 0 à 127. | |||
* l'octet: représente des nombres de 0 à 255. C'est souvent une unité de base utilisée avec des multiples. Il est exactement écrit avec deux chiffres hexadécimaux. | |||
Les entiers de taille plus grandes sont représenté dans des suites d'octets: | Les entiers de taille plus grandes sont représenté dans des suites d'octets: | ||
* l'entier court (short, shortint, int16): 2 octets. De 0 à 65535. | |||
* l'entier: (int, integer, int32): 4 octets. De 0 à 2^32-1. | |||
* l'entier long (long, int64): 8 octets. De 0 à 2^64-1. | |||
* l'entier long long, ou entier géant (bigint, int128): 16 octets. De 0 à 2^128-1. | |||
Selon les processeurs les bits sont disposés en mémoire en partant du bit le plus significatif ou bien du moins significatif. Nous parlerons ainsi de MSB pour "most significant bit" et LSB pour "less significant bit". | Selon les processeurs les bits sont disposés en mémoire en partant du bit le plus significatif ou bien du moins significatif. Nous parlerons ainsi de MSB pour "most significant bit" et LSB pour "less significant bit". | ||
| Ligne 51 : | Ligne 53 : | ||
Le mot: il est possible que vous rencontrerez ce terme dans de la documentation informatique. Il s'agit ici du mot machine. Il s'agit du nombre le plus grand qu'un processeur soit capable de manipuler à chaque instruction élémentaire. Ainsi un processeur de 32 bits est capable de manipuler des nombres entiers de 32 bits. | Le mot: il est possible que vous rencontrerez ce terme dans de la documentation informatique. Il s'agit ici du mot machine. Il s'agit du nombre le plus grand qu'un processeur soit capable de manipuler à chaque instruction élémentaire. Ainsi un processeur de 32 bits est capable de manipuler des nombres entiers de 32 bits. | ||
== Les entiers négatifs == | |||
Jusqu'ici nous n'avons parlé que des entiers positifs. Or les unités arithmétiques des processeurs sont capables de manipuler des entiers négatifs. Comment fait-on pour les représenter ? | Jusqu'ici nous n'avons parlé que des entiers positifs. Or les unités arithmétiques des processeurs sont capables de manipuler des entiers négatifs. Comment fait-on pour les représenter ? | ||
Et bien nous utilisons le bit le plus significatif pour indiquer qu'un nombre est négatif (1) ou positif (0). | Et bien nous utilisons le bit le plus significatif pour indiquer qu'un nombre est négatif (1) ou positif (0). | ||
| Ligne 57 : | Ligne 59 : | ||
Mais comment fait-on pour différencier les entiers avec ou sans signes ? Dans l'absolu on ne sait pas faire la différence. Seul les programmes savent comment convertir ces nombres pour l'afficher correctement. | Mais comment fait-on pour différencier les entiers avec ou sans signes ? Dans l'absolu on ne sait pas faire la différence. Seul les programmes savent comment convertir ces nombres pour l'afficher correctement. | ||
== L'hexadécimal == | |||
On peut parler aussi de la base 16. Les chiffres sont : 0 à 9, puis a, b, c, d, e et f. Les lettres peuvent être en minuscule ou en majuscule. Cela n'a pas d'importance. | On peut parler aussi de la base 16. Les chiffres sont : 0 à 9, puis a, b, c, d, e et f. Les lettres peuvent être en minuscule ou en majuscule. Cela n'a pas d'importance. | ||
Cette base est très souvent employée. Elle a l'avantage d'être compacte, explicite et fixe. Un octet sera toujours représenté par 2 chiffres hexa. | Cette base est très souvent employée. Elle a l'avantage d'être compacte, explicite et fixe. Un octet sera toujours représenté par 2 chiffres hexa. | ||
| Ligne 63 : | Ligne 65 : | ||
Pour convertir de l'hexa vers le décimal: pour chaque chiffre on multiplie le nombre en décimal par une puissance de 16 en fonction de sa position. | Pour convertir de l'hexa vers le décimal: pour chaque chiffre on multiplie le nombre en décimal par une puissance de 16 en fonction de sa position. | ||
Exemples (le plus significatif est à gauche): | Exemples (le plus significatif est à gauche): | ||
* 8a: 10 + 16 * 8 = 138 | |||
* af: 15 + 16 * 10 = 175 | |||
* 3fea: 10 + 14 * 16 + 15 * 16 * 16 + 3 * 16 * 16 * 16 = 16362 | |||
== Les nombres décimaux == | |||
Ici nous allons retrouver différentes façons de stocker les nombre décimaux. | |||
=== A virgule fixe === | |||
Le principe est simple. En prend un nombre entier et on déplace la virgule d'autant de chiffre que souhaité. | |||
Pour savoir comment est placé le séparateur décimal, seul le programme sait. Il s'agit d'une convention pour savoir combien de chiffres on place après la virgule. | |||
L'avantage de cette façon de faire est que les additions et les soustractions sont exactes. Le principal inconvénient est qu'on ne peut pas stocker des nombres très très grands. L'espace de stockage est directement proportionnel au nombre de chiffres à stocker. | |||
On utilise ce format essentiellement pour la finance et la comptabilité ou la précision est importante. | |||
=== A virgule flottante === | |||
Bon là, ça se complique. L'objectif de ce format est de pouvoir stocker des nombres de grande taille en prenant le moins de place possible. On utilise pour cela le format IEEE. Vous pouvez consulter la page [https://fr.wikipedia.org/wiki/IEEE_754 Wikipédia] pour plus d'informations. | |||
Pour la base, dans une série d'octets on stocke les informations pour reconstituer le nombre. Les différents parties sont: le signe (1 bit), la mantisse et l'exposant. | |||
Vous commencer à percevoir le problème que cela pose ? Il s'agit d'une approximation du nombre de départ. D'une part à cause de la mantisse qui perd les chiffres les moins significatifs et d'autres part à cause de l'exposant qui fonctionne en base 2. Ainsi des nombre comme 1, 3, ou 10 ne sont pas stockés comme tels. | |||
Version actuelle datée du 2 septembre 2022 à 13:58
Les système de numération
Le binaire
Le processeur en lui-même ne gère que des bits. On dit qu'il utilise le système binaire. On résume souvent au zéro (0) et au un (1) pour distinguer les deux états. Ceci est bien pratique pour réaliser des calculs. Toutefois on parlerait plutôt d'état actif et d'état repos. On associe le 1 à l'état actif et le 0 à l'état repos.
Par exemple :
- La porte serait ouverte ou fermée
- La lumière serait allumée ou éteinte
- Le niveau de l'eau serait haut ou bas
- etc.
Une algèbre existe pour manipuler et combiner ces valeurs. Il s'agit de l'algèbre de Boole.
A là base il existe trois opérateurs: le ET, le OU et le NON. D'autres opérateurs existent mais en réalité ils peuvent être construit à partir des 3 précédents: XOU ou OU exclusif, NAND ou NOT AND, IMP ou implication.
Le ET logique
La sortie du ET est vraie si et seulement si les 2 entrées sont vraies.
Il est souvent noté par le point.
Le OU logique
La sortie du OU est vraie si et seulement si l'une des 2 entrées au moins est vraie.
Il est souvent noté par le signe plus (+).
Le NON logique
La sortie du NON est toujours l'opposé de l'entrée.
Il est représenté par une barre horizontale au-dessus de l'expression.
Les entiers
Une succession de 0 et de 1 c'est bien joli, mais ce n'est pas trop parlant pour un humain qui à l'habitude de manipuler les nombres en base décimale.
Pour stocker des nombre entiers nous utilisons des regroupements de bits:
- le tercet: permet de représenter des chiffres de 0 à 7 en base octale (base 8).
- le quartet: permet de représenté un chiffre hexadécimal de 0 à F (0 à 15 en décimal).
- le septet: représente des nombres de 0 à 127.
- l'octet: représente des nombres de 0 à 255. C'est souvent une unité de base utilisée avec des multiples. Il est exactement écrit avec deux chiffres hexadécimaux.
Les entiers de taille plus grandes sont représenté dans des suites d'octets:
- l'entier court (short, shortint, int16): 2 octets. De 0 à 65535.
- l'entier: (int, integer, int32): 4 octets. De 0 à 2^32-1.
- l'entier long (long, int64): 8 octets. De 0 à 2^64-1.
- l'entier long long, ou entier géant (bigint, int128): 16 octets. De 0 à 2^128-1.
Selon les processeurs les bits sont disposés en mémoire en partant du bit le plus significatif ou bien du moins significatif. Nous parlerons ainsi de MSB pour "most significant bit" et LSB pour "less significant bit".
Le mot: il est possible que vous rencontrerez ce terme dans de la documentation informatique. Il s'agit ici du mot machine. Il s'agit du nombre le plus grand qu'un processeur soit capable de manipuler à chaque instruction élémentaire. Ainsi un processeur de 32 bits est capable de manipuler des nombres entiers de 32 bits.
Les entiers négatifs
Jusqu'ici nous n'avons parlé que des entiers positifs. Or les unités arithmétiques des processeurs sont capables de manipuler des entiers négatifs. Comment fait-on pour les représenter ? Et bien nous utilisons le bit le plus significatif pour indiquer qu'un nombre est négatif (1) ou positif (0).
Mais comment fait-on pour différencier les entiers avec ou sans signes ? Dans l'absolu on ne sait pas faire la différence. Seul les programmes savent comment convertir ces nombres pour l'afficher correctement.
L'hexadécimal
On peut parler aussi de la base 16. Les chiffres sont : 0 à 9, puis a, b, c, d, e et f. Les lettres peuvent être en minuscule ou en majuscule. Cela n'a pas d'importance. Cette base est très souvent employée. Elle a l'avantage d'être compacte, explicite et fixe. Un octet sera toujours représenté par 2 chiffres hexa.
Pour convertir de l'hexa vers le décimal: pour chaque chiffre on multiplie le nombre en décimal par une puissance de 16 en fonction de sa position. Exemples (le plus significatif est à gauche):
- 8a: 10 + 16 * 8 = 138
- af: 15 + 16 * 10 = 175
- 3fea: 10 + 14 * 16 + 15 * 16 * 16 + 3 * 16 * 16 * 16 = 16362
Les nombres décimaux
Ici nous allons retrouver différentes façons de stocker les nombre décimaux.
A virgule fixe
Le principe est simple. En prend un nombre entier et on déplace la virgule d'autant de chiffre que souhaité. Pour savoir comment est placé le séparateur décimal, seul le programme sait. Il s'agit d'une convention pour savoir combien de chiffres on place après la virgule.
L'avantage de cette façon de faire est que les additions et les soustractions sont exactes. Le principal inconvénient est qu'on ne peut pas stocker des nombres très très grands. L'espace de stockage est directement proportionnel au nombre de chiffres à stocker.
On utilise ce format essentiellement pour la finance et la comptabilité ou la précision est importante.
A virgule flottante
Bon là, ça se complique. L'objectif de ce format est de pouvoir stocker des nombres de grande taille en prenant le moins de place possible. On utilise pour cela le format IEEE. Vous pouvez consulter la page Wikipédia pour plus d'informations.
Pour la base, dans une série d'octets on stocke les informations pour reconstituer le nombre. Les différents parties sont: le signe (1 bit), la mantisse et l'exposant. Vous commencer à percevoir le problème que cela pose ? Il s'agit d'une approximation du nombre de départ. D'une part à cause de la mantisse qui perd les chiffres les moins significatifs et d'autres part à cause de l'exposant qui fonctionne en base 2. Ainsi des nombre comme 1, 3, ou 10 ne sont pas stockés comme tels.